The pentagon is a captivating geometric shape with five sides and five angles. Its characteristics make it an essential subject in mathematics and a prominent figure in various applications, from engineering and architecture to art and nature. Although the phrase math:rb6-qld747y= pentagon does not convey a known concept in mathematics, it leads us to a deeper understanding of pentagons and their significance across multiple disciplines.
Unraveling Math:rb6-qld747y= Pentagon
The expression math:rb6-qld747y= pentagon does not correlate to a standard term in mathematical literature. It might serve as a symbolic representation or a coded reference. While the significance of math:rb6-qld747y= pentagon remains uncertain, the focus on the word “pentagon” allows for a detailed examination of its role in geometry and beyond.
Defining a Pentagon and Its Varieties
A pentagon is a polygon that consists of five sides and five angles. Pentagons can be categorized as:
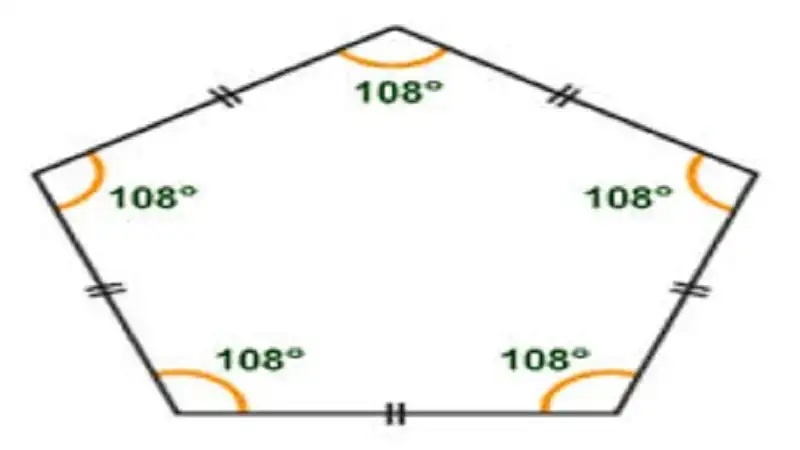
- Regular Pentagon: Features five equal sides and five equal angles, with each interior angle measuring 108∘108^\circ.
- Irregular Pentagon: Consists of sides and angles of different lengths and measurements, allowing for diverse shapes.
- Convex Pentagon: All interior angles are less than 180∘180^\circ, with vertices pointing outward.
- Concave Pentagon: Has at least one interior angle greater than 180∘180^\circ, resulting in a “caved-in” appearance.
These distinctions are important for understanding how pentagons behave in various mathematical contexts and real-world scenarios.
Geometric Properties of a Regular Pentagon
Interior and Exterior Angles Calculation
For any polygon, the sum of its interior angles can be calculated using the formula:
Sum of interior angles=(n−2)×180∘\text{Sum of interior angles} = (n-2) \times 180^\circ
where nn represents the number of sides. For a pentagon (n=5n = 5):
(5−2)×180∘=540∘(5-2) \times 180^\circ = 540^\circ
Therefore, each interior angle in a regular pentagon is:
540∘/5=108∘540^\circ / 5 = 108^\circ
The sum of the exterior angles of any polygon is always 360∘360^\circ. Thus, each exterior angle of a regular pentagon measures:
360∘/5=72∘360^\circ / 5 = 72^\circ
A pentagon has five diagonals, which are line segments connecting non-adjacent vertices. The diagonals in a regular pentagon intersect each other at points that divide them in the golden ratio, revealing a deep connection between pentagons and this famous mathematical proportion.
Area and Perimeter Formulas for Regular Pentagons
To find the area of a regular pentagon with side length ss, the formula is:
Area=145(5+25)s2\text{Area} = \frac{1}{4} \sqrt{5(5 + 2\sqrt{5})} s^2
This equation provides a precise measure of the space within the pentagon’s boundaries. The perimeter of a pentagon is straightforward to calculate:
Perimeter=5s\text{Perimeter} = 5s
Professionals frequently apply these formulas in fields such as architecture and engineering, using pentagon-based designs for aesthetic and functional purposes.
Real-World Applications of Pentagons
Architecture and Structural Design
Pentagons appear in architectural structures due to their unique properties and visual appeal. One famous example is the Pentagon building in Washington, D.C., which serves as the U.S. Department of Defense headquarters. The building’s pentagonal shape optimizes space and symbolizes strength and unity. In addition, pentagonal designs are often employed in constructing floor plans, windows, and roof structures to achieve aesthetic harmony.
Role in Art and Design
In art, pentagons frequently emerge in patterns, tessellations, and symbolic representations. The five-fold symmetry of a regular pentagon makes it suitable for creating balanced and visually pleasing designs. Artists and designers use pentagons in logos, motifs, and even modern digital design tools.
Pentagons in Mathematical Theories and Concepts
Pentagonal Numbers
Pentagonal numbers are figurate numbers that extend the concept of triangular and square numbers. The formula for finding the nn-th pentagonal number is:
Pn=3n2−n2P_n = \frac{3n^2 – n}{2}
These numbers have applications in number theory, particularly in partition theory, where they help in the study of integer partitions.
Geometric Puzzles
Pentagons present intriguing challenges in geometric puzzles and problems, such as finding optimal packing solutions or exploring the relationships between diagonals, sides, and angles. These problems often require creative thinking and advanced mathematical skills.
Symmetry and Rotational Properties of Regular Pentagons
Regular pentagons exhibit both rotational symmetry (order 5) and reflectional symmetry. This means a regular pentagon can be rotated by multiples of 72∘72^\circ and still look the same. These symmetry properties make pentagons ideal for studying concepts in group theory and crystallography, where symmetry plays a central role.
Occurrences of Pentagons in Nature
Biological Examples
In nature, pentagonal symmetry is found in various biological forms, such as flowers with five petals, sea stars with five arms, and certain fruits. These examples illustrate the prevalence of five-fold symmetry in living organisms, often linked to optimal growth and reproduction strategies.
Connection with the Golden Ratio
The golden ratio, denoted by ϕ≈1.618\phi \approx 1.618, has a special relationship with pentagons. In a regular pentagon, the ratio of a diagonal to a side equals the golden ratio. This mathematical connection is frequently observed in natural patterns and proportions, including the spiral arrangement of leaves on plants, known as phyllotaxis.
Pentagon Tessellation Possibilities
Tessellation involves covering a surface without gaps or overlaps using one or more shapes. While regular pentagons cannot tessellate on their own, certain types of irregular pentagons can. Some convex and non-convex pentagons possess the ability to tile a plane, creating fascinating and intricate patterns. These tessellation properties are of interest in fields such as art, architecture, and even molecular chemistry.
Advanced Mathematical Problems Involving Pentagons
Pentagons appear in a variety of complex mathematical problems, ranging from geometric puzzles to number theory:
- Pentagonal Number Theorem: This theorem in number theory is significant in the study of partitions, particularly regarding the distribution of integers.
- Geometric Optimization Problems: Problems involving pentagons often deal with maximizing area, minimizing perimeter, or finding ideal packing arrangements, which are critical in fields like materials science.
Pentagons in Technology and Engineering
It find use in technology and engineering due to their structural properties. Examples include:
- Satellite Dishes and Antennas: Certain antenna designs incorporate pentagonal elements for optimizing signal coverage.
- Materials Science: In nanotechnology and materials engineering, pentagon-based structures help create stable frameworks for new materials.
Symbolic and Cultural Significance of Pentagons
Pentagons carry various symbolic meanings across cultures:
- Ancient Civilizations: The pentagon and pentagram were symbols of health and life in ancient Greece.
- Western Occultism: The pentagram is a prominent symbol in Western esoteric traditions, representing protection, spirituality, and magic.
- Religious Symbolism: In some Eastern philosophies, the pentagon represents the five elements: earth, water, fire, air, and space.
These symbolic meanings reflect the pentagon’s enduring cultural significance, extending beyond its mathematical properties.
Common Misconceptions About Pentagons
A widespread misconception is that all pentagons are regular, or that pentagonal shapes must have equal sides and angles. In reality, pentagons come in diverse forms, including irregular and concave shapes. Recognizing this diversity is crucial for accurately applying geometric principles and understanding pentagon-related problems in mathematics and engineering.
Conclusion: The Broader Impact of Pentagons
Pentagons are not just five-sided figures—they are fundamental to geometry, art, and even natural science. From the architecture of the Pentagon building to the patterns in flowers and the complexities of mathematical theorems, pentagons occupy a central role across disciplines. Their properties, symbolic meanings, and practical applications make pentagons an essential subject in education, research, and creative fields.
Read More beautydod.
FAQs
1.How are pentagons used in architecture?
Architects employ pentagons in building designs for aesthetic appeal and space optimization, such as in the Pentagon building in the U.S
2.Can pentagons appear in nature?
Yes, pentagons are common in nature, found in flowers, starfish, and patterns that follow the golden ratio.
3.What are pentagonal numbers?
Pentagonal numbers are a sequence of numbers derived from the formula Pn=3n2−n2P_n = \frac{3n^2 – n}{2}, important in number theory.
4.Are there real-world applications for irregular pentagons?
Irregular pentagons are used in tiling, pattern design, and even in molecular structures to create stable frameworks.
5.Why is a pentagon significant in different cultures?
In many traditions, the pentagon and pentagram are symbols of balance, protection, and the natural elements, reflecting deep cultural significance.